No uso de dados geofísicos, assim como ocorre em outros tipos de dados, é preciso atentar para algumas limitações, tanto da técnica em si, como limitações ligadas à distribuição espacial dos pontos que contém dados. Chamamos de resolução espacial o menor tamanho de célula possível de ser utilizado. A resolução espacial é uma questão crítica para qualquer interpretação, para não haver o risco de caracterizar uma feição geológica que não poderia ser contemplada pelo dado utilizado.
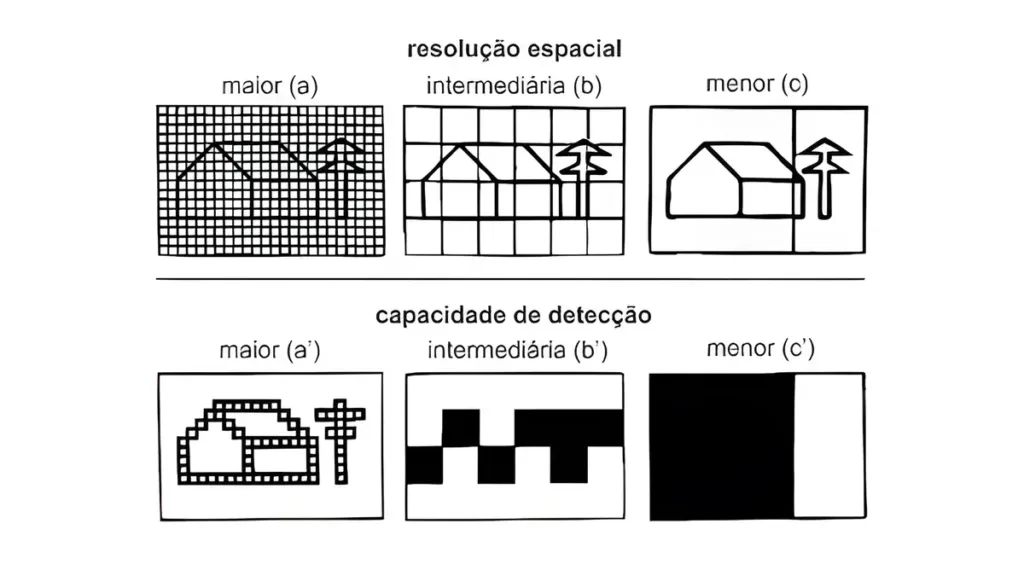
Na imagem a seguir, há uma representação do impacto da diminuição da resolução espacial (de a para c) na definição de um alvo aleatório. Observamos que todos os valores que estiverem dentro de uma célula (valores de uma determinada propriedade) serão somados, resultando em um valor único. Assim, podemos imaginar que, quanto menor a resolução espacial, menor a capacidade de identificar o alvo pretendido.
Um famoso padrão matemático é aplicado quando falamos em resolução de dados geofísicos: o Teorema de Nyquist. Segundo este teorema, para uma distância entre pontos com dados observados (∆𝑥), o menor comprimento de onda possível de ser registrado (𝑇𝑁) equivale a 2 ∗ ∆𝑥. Desta definição é que sai a conclusão de que o menor tamanho de célula confiável para representar um dado formado por ondas, que é o caso dos dados de métodos potenciais, é metade do tamanho do espaçamento entre amostras.
Mas quando estamos lidando com dados geofísicos, temos algumas restrições de disponibilidade de dados, e então são realizadas algumas concessões. Com os dados terrestres, comumente há regiões que não são cobertas por dados. Porém, é comum realizar algum tipo de técnica de interpolação para cobrir o “vazio” de dados. Isto pode facilitar a interpretação geológica, mostrando tendências de grande escala, mas é importante que os mapas venham acompanhados com a marcação dos pontos onde há dados reais.
No caso dos dados aéreos, há uma taxa de amostragem muito alta ao longo das linhas de voo, e uma sub-amostragem na direção transversal. Neste caso, se forem usados espaçamento menores que metade da distância das linhas de produção, haverá um efeito de geração de anomalias que não existem, um efeito conhecido como aliasing. Já ao longo das linhas, também há um aliasing, mas resultante da criação de anomalias de maior comprimento de onda como resultado da super amostragem. Uma opção é remover valores ao longo das linhas, para realizar a interpolação de acordo com o Teorema de Nyquist, mas isto não é comum. Por outro lado, é uma prática comum a aplicação de espaçamentos em torno de 1/3, 1/4 ou 1/5 da distância entre as linhas, como forma de balancear o efeito de aliasing entre linhas e ao longo destas.
