O nome “métodos potenciais” se refere ao estudo e aplicação de técnicas para estudar o campo magnético e o campo gravimétrico terrestres. Este termo só se aplica a estes dois métodos, porque toda a base científica deste tipo de estudo está fundada no estudo de campo potencial. Isso fica mais fácil de entender sabendo o que é um campo potencial!
O que é campo potencial?
Primeiro, o conceito de “campo”. Quando falamos em “campo”, ou “campo de força”, não é aquela bolha que os heróis fictícios fazem quando fazem um escudo de energia, ou algo assim. O campo, na verdade, permeia todo o espaço fora da superfície de sua fonte, e só é zero no infinito.Dizemos que há um campo quando há um padrão coerente de distribuição de valores no espaço, de alguma propriedade física desse meio.
No caso da gravidade, por exemplo, imagine que cada ponto do espaço onde você está tem um valor que se refere à gravidade. No entorno da Terra, os valores se tornam mais altos quanto mais próximos da superfície do planeta. Então, o valor do campo é maior nos seus pés do que na sua cabeça, por exemplo.
No caso da gravimetria e da magnetometria, os campos de força estudados são dados pela variação no espaço dos valores de potencial magnético e gravimétrico.
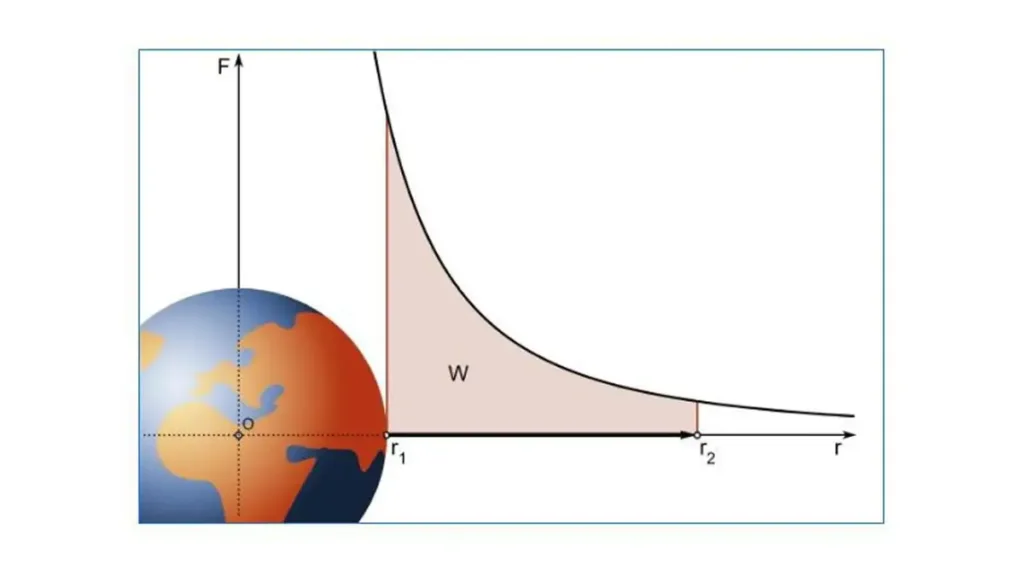
Em campos potenciais, consideramos também o trabalho realizado (representado por W) para levar um corpo, que interage com esse campo, de um ponto (r1) a outro ponto (r2).
No espaço, o campo potencial é invisível, mas podemos representa-lo por desenhos. Se fizermos setas desde regiões mais fracas até regiões mais fortes, dando a direção para onde os valores aumentam, estaremos desenhando o campo, as “linhas de campo”.
Desenhar as linhas de campo nos dá uma boa visão sobre como o campo se comporta no espaço. Isso permite prever as trajetórias de corpos dentro do campo, pois estes sempre se moverão das regiões de alta energia potencial para as regiões de baixa energia potencial, seguindo estas linhas.
Linhas de campo do campo gravitacional da Terra, e do campo geomagnético. Até aqui falamos de campo potencial gravimétrico. Isto porque temos que começar do mais simples para o mais difícil. E, estudar o campo magnético, é um pouco (muito?) mais complicado do que estudar o campo gravimétrico. Enquanto a gravidade é um campo monopolar, ou seja, possui um ponto central para onde as linhas de campo convergem, o campo magnético é dipolar. Além disso, apesar dos dois campos possuírem variações no tempo, o campo geomagnético varia muito mais.
E “o buraco é mais embaixo”.
Pensando na explicação física do que é campo potencial, o campo magnético não seria um campo potencial. Isso porque o campo magnético global é, em grande parte, um dipolo magnético. Por isso as linhas de campo são as de um dipolo, e circulam (por isso, o rotacional do campo não é zero). Mas não vamos mergulhar em Equações de Maxwell e afins aqui. O importante agora é saber que o campo magnético é considerado campo potencial porque a variação de sua forma mais global é lenta, e pode ser aproximada para um campo mais “fixo” dentro de um intervalo de tempo. Essa representação é o chamado IGRF (International Geomagnetic Reference Model). Mas, como o campo geomagnético não é estático, o IGRF é atualizado a cada 5 anos.
Veja que a gravimetria e a magnetometria trata do estudo dos dois campos de força planetários que temos. Com todo este contexto de campo planetário, entende porque não devemos chamar gamaespectrometria e outros métodos geofísicos de “potenciais”? São outros tipos de processos físicos.
Aprofundando no tema – Alguns conceitos físicos
- O campo potencial vetorial é obtido fazendo o gradiente no espaço do campo potencial (escalar). A letra grega nabla (∇) é usada para o operador gradiente. Então, se V representa a energia potencial em um certo ponto do campo, o campo potencial () é o gradiente de V, representado por -∇V. O campo potencial é negativo quando os valores aumentam em direção à fonte.
- O campo potencial fornece uma maneira de calcular o trabalho realizado por uma força conservativa. Quando uma partícula se move de um ponto r1 para um ponto r2, dentro de um campo conservativo, o trabalho realizado pela força estudada será igual à diferença entre os valores do campo potencial nos dois pontos (∆V), ou seja, W = ∆V = V(r1) – V(r2).
